tosses <- do (10000) * rflip(3)
gf_props(~heads, data=tosses)Math 132B
Class 12
Definition of a Random Variable
A random variable is a mathematical model of a random quantity (measurement, count)
It is a function that assigns each outcome from a sample space a number.
Example: The number of dots on the side of a die that is facing up.
Example: The total number of dots on the sides of two dice that are facing up.
Example: The number of infants that choose the friendly character.
Example: The height of a plant randomly selected from a field.
Example
Example
-
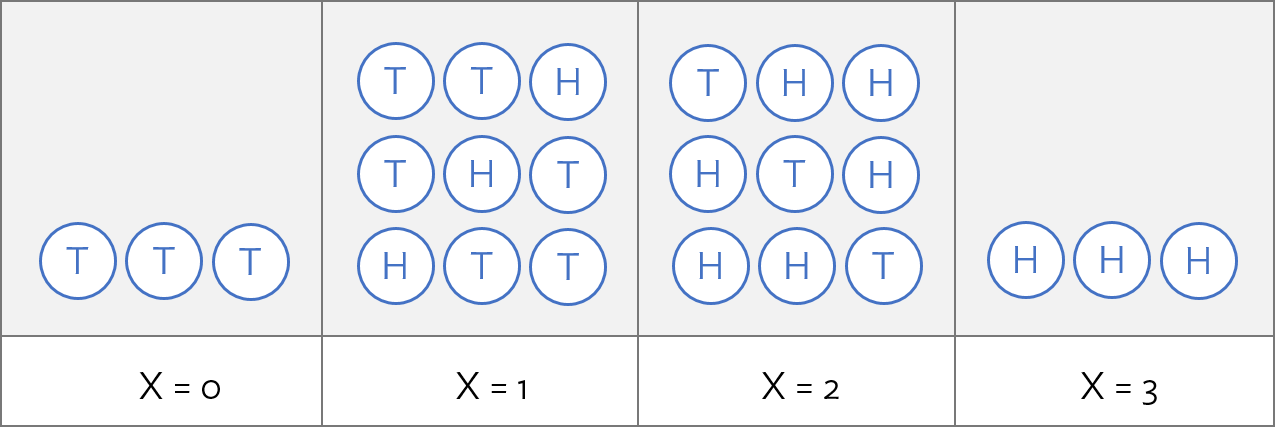
3 coin tosses
More examples:
Taking a token 3 times from a bag with one red and one blue token, with replacement. Counting the number of red tokens.
Asking 3 people to randomly select one of two characters, when they have no preference. Counting the number of times the friendly character was selected.
Randomly selecting 3 people from a large crowd that has 50% males and 50% females. Counting the number of females.
Randomly selecting 3 plants from a field in which 50% of the plants have some specific genetic mutation. Counting the number of plants with the mutation.
Mathematically, all of those are the same.
Distribution of a Random Variable
The distribution of a discrete random variable is the collection of its values and the probabilities associated with those values.
The probability distribution for
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1/8 | 3/8 | 3/8 | 1/8 |
The probabilities must add up to 1
Bar graph showing a distribution
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1/8 | 3/8 | 3/8 | 1/8 |
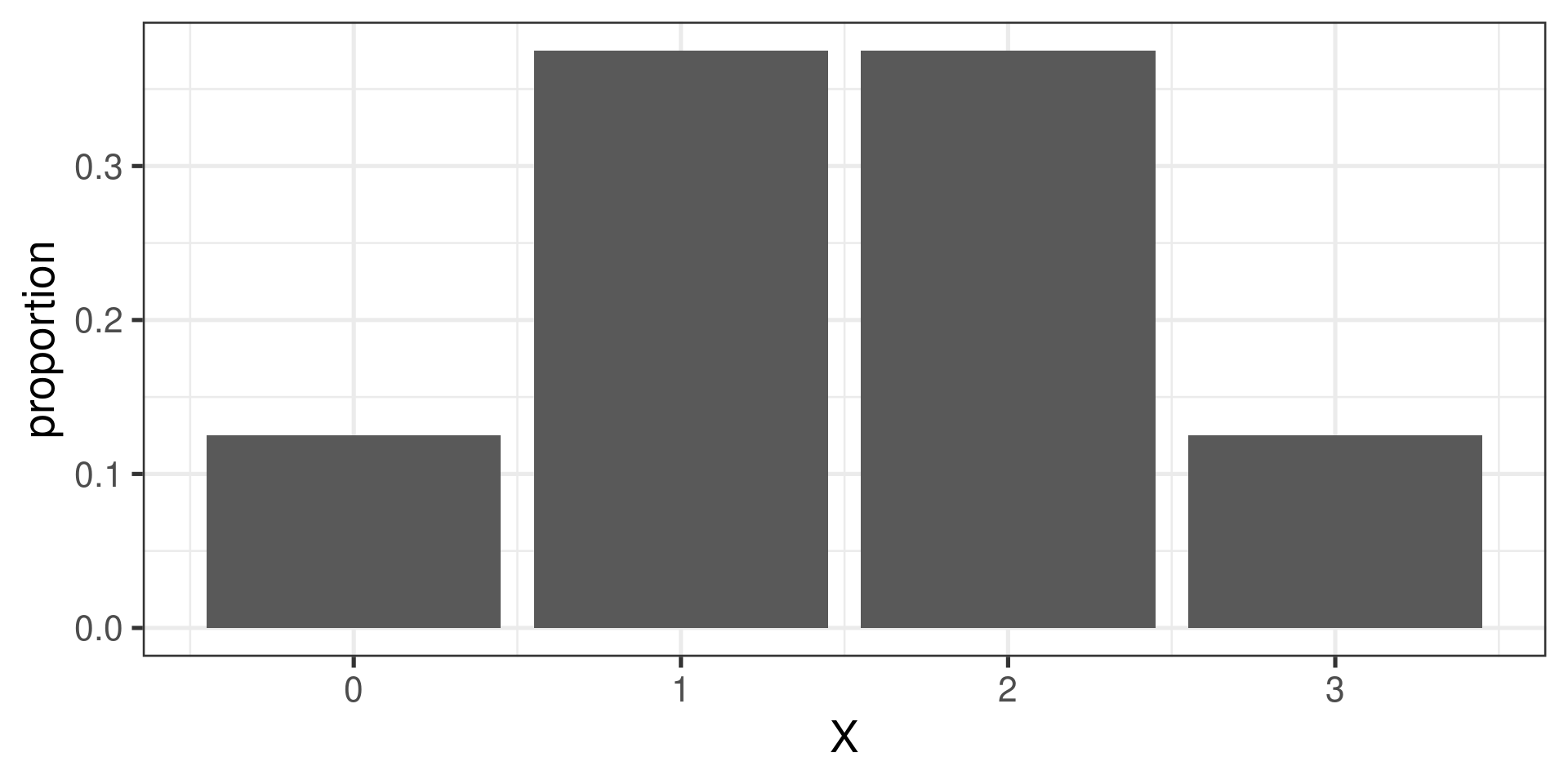
Using a simulation to approximate a probability distribution
Expectation of a Random Variable
If
The Greek letter
Expectation…
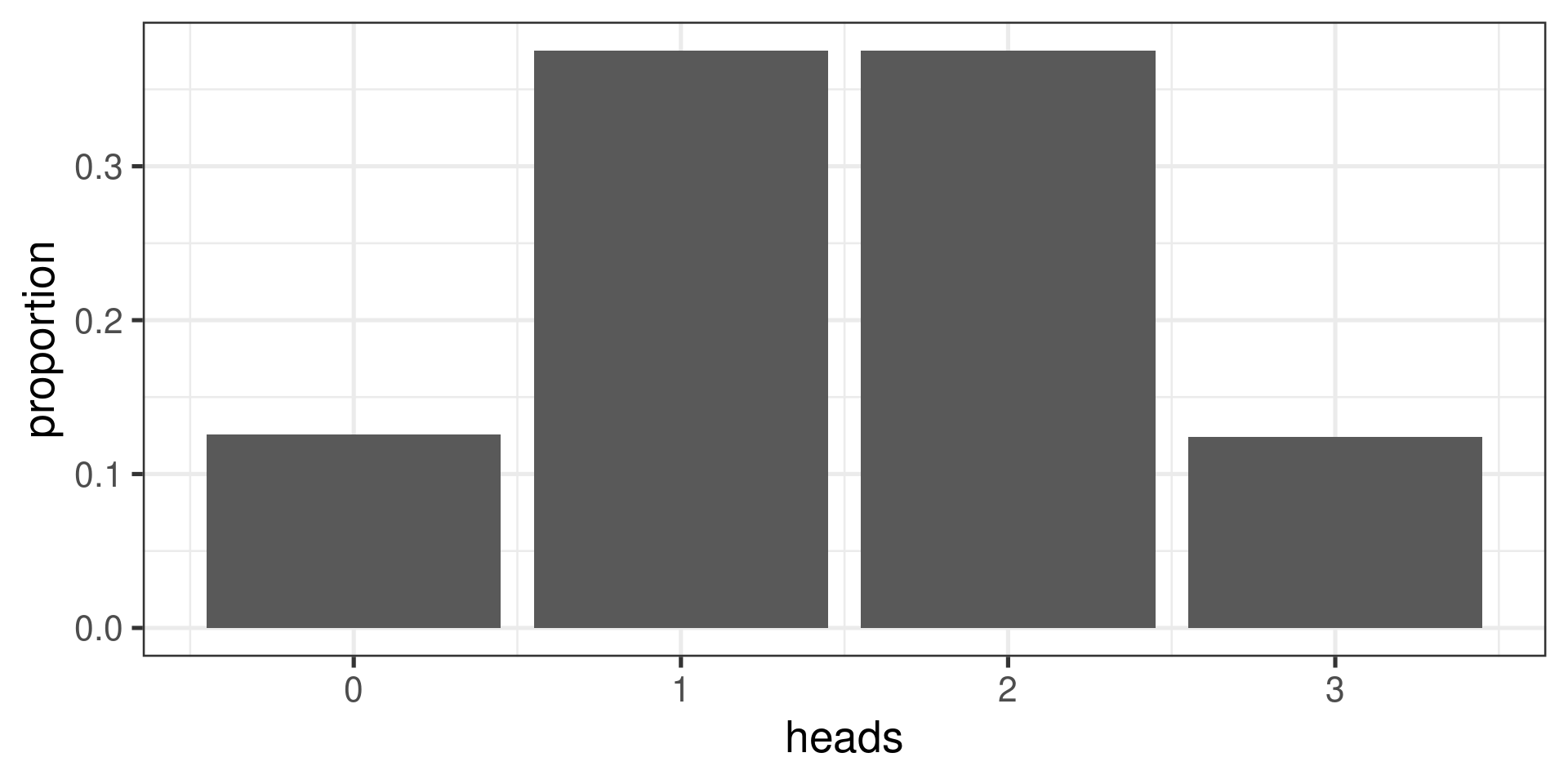
In the coin tossing example,
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
Expectation…
Intuitively, the expected value of
tosses <- do (10000) * rflip(3)
mean(~heads, data=tosses)[1] 1.4923Variance and SD of a Random Variable
If
The standard deviation of
Variance and SD…
In the coin tossing example,
| 0 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 1/8 | 3/8 | 3/8 | 1/8 |
The standard deviation
Standard Deviation …
Again, the standard deviation of
tosses <- do (10000) * rflip(3)
sd(~heads, data=tosses)[1] 0.8643192Another example
Suppose your roll three fair six sided dice. Let
What are the possible values of
What is the probability distribution for
What is the expected value of
What is the variance of
Common theme
- Number of heads when tossing three fair coins
- Number of sixes when rolling three fair dice
- Number of heads when tossing 16 fair coins
- Number of infants choosing the helper, provided infants choose randomly.
All these can be modeled by so-called binomial random variables.
Binomial Random Variables
- Each replicate is independent of the other replicates.
- Each replicate has two possible outcomes: either success or failure.
- The probability of success
This is also called a binomial process.
A binomial random variable takes on values
The numbers
We write
The Binomial Distribution
Suppose
-
-
-
But also
or it may be that the first is success, then there are two failures, then a success, and so on.
How many different ways can we choose
The Binomial Coefficient
The binomial coefficient
Mathematically,
Examples
- Calculate
- Calculate
- Calculate
- Calculate
Formula for the binomial distribution
Let
Parameters of the distribution:
Examples
-
Let
Calculate
-
Let
Calculate
-
Let
Calculate
(Hint:
Mean and SD for a binomial random variable
For a binomial distribution with parameters
Mean =
Standard Deviation =
The derivation is not shown here nor in the text; it will not be asked for on a problem set or exam.
Binomial Probabilities in R
The function dbinom() is used to calculate
dbinom(k, size=n, prob=p):
For example, if
dbinom(2, size=3, prob=1/6)[1] 0.06944444The d in dbinom stands for distribution or density.
Binomial Probabilities in R …
The function pbinom() is used to calculate
-
pbinom(k, size=n, prob=p) -
pbinom(k, size=n, prob=p, lower.tail = FALSE)
The p stands for probability.
pbinom examples:
if
pbinom(13, size=16, prob=1/2)[1] 0.9979095while
pbinom(13, size=16, prob=1/2, lower.tail=FALSE)[1] 0.002090454or, equivalently:
1 - pbinom(13, size=16, prob=1/2)[1] 0.002090454