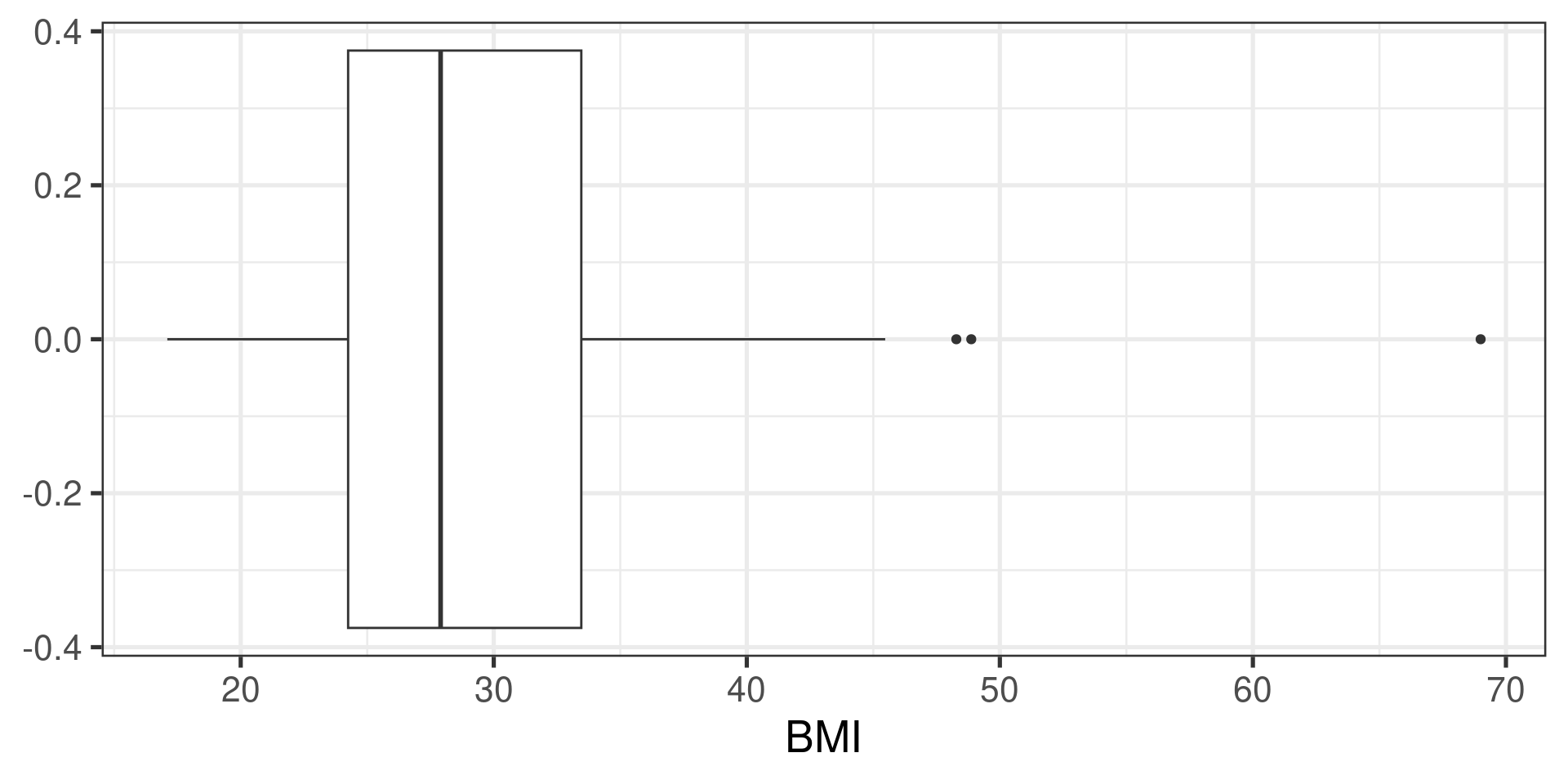
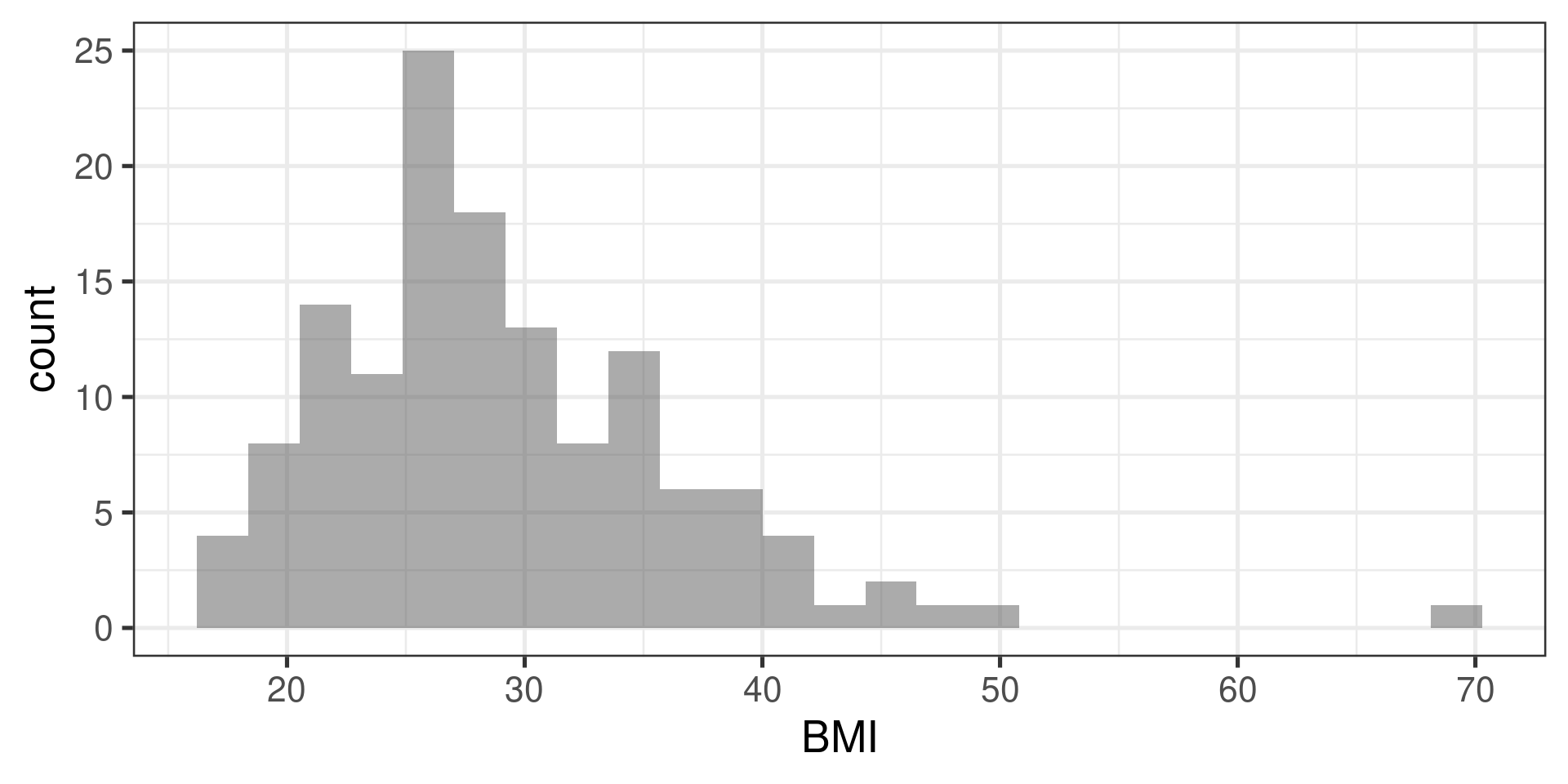
min Q1 median Q3 max mean sd n missing
17.1 24.245 27.9 33.46 69 29.09956 7.552866 135 0Math 132B
Class 18
Falsifying mathematical models
Do Americans tend to be overweight?
Body mass index (BMI) is an approximate scale used to assess weight status that adjusts for height.
When weight is measured in kg and height in meters,
When weight is measured in lbs and height in inches,
WHO standards for BMI
| Category | BMI range |
|---|---|
| Underweight | |
| Normal (healthy weight) | 18.5-24.99 |
| Overweight | |
| Obese |
The National Health and Nutrition Survey (NHANES)
The National Health and Nutrition Examination Survey (NHANES) is another survey conducted by the CDC.
Purpose: to assess the health and nutritional status of adults and children in the United States
The
NHANESdataset in theNHANESpackage contains responses from 10,000 participants.The
nhanes.samp.adultdataset in theoibiostatpackage contains responses from a random sample from participants who were age 21 or older.
We will treat nhanes.samp.adult as our sample and think of the adult participants in the NHANES dataset as the population.
The NHANES sample
The NHANES sample…
Two approaches to the problem
I. Calculate a confidence interval for the population mean BMI.
- Use the formal logic of hypothesis testing.
I. Calculating a 95% confidence interval
- Calculate sample mean
- Calculate sample standard deviation
- Figure out the sample size
- Plug into the formula.
min Q1 median Q3 max mean sd n missing
17.1 24.245 27.9 33.46 69 29.09956 7.552866 135 0I. Calculating a 95% confidence interval
Critical t
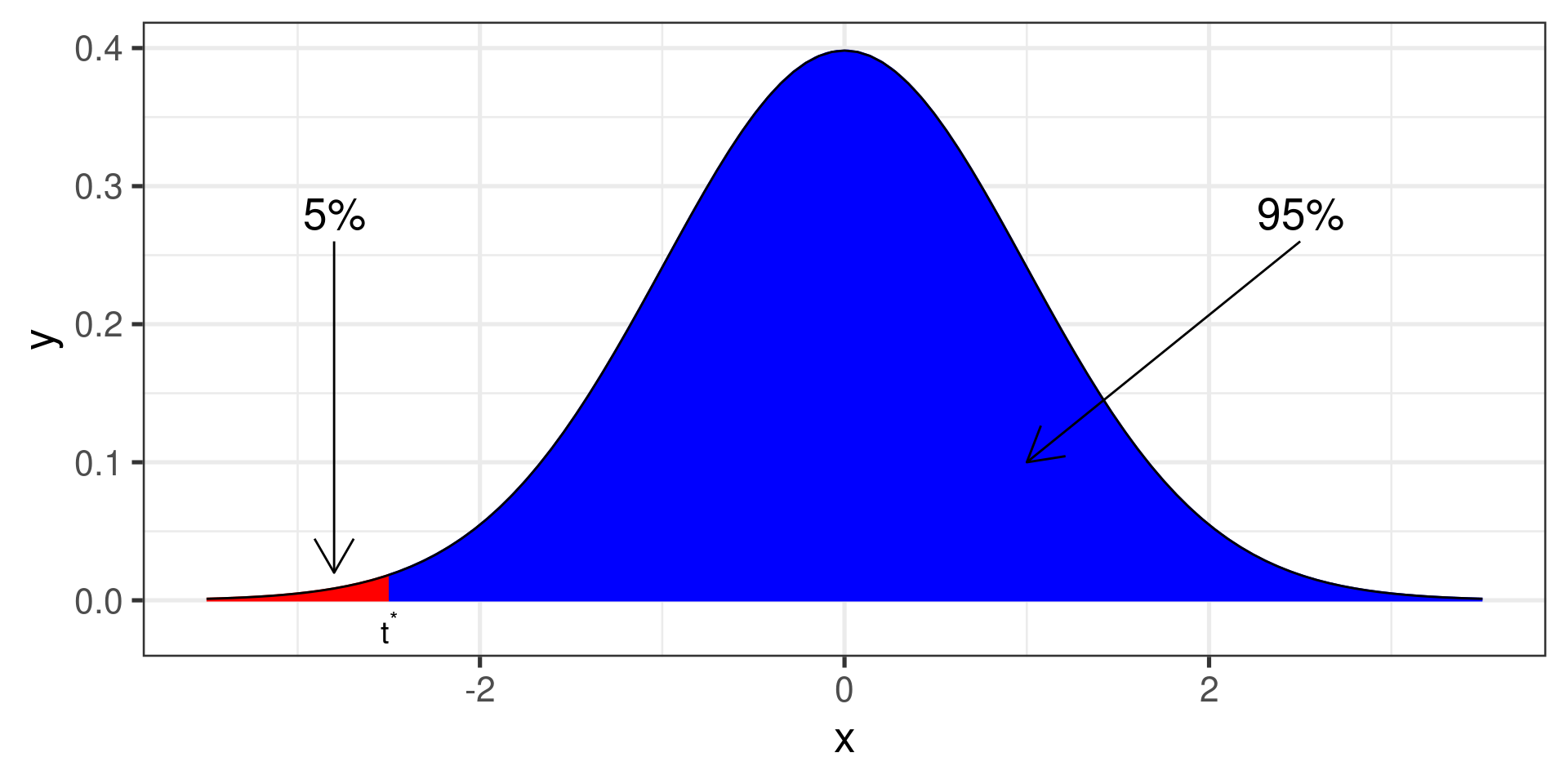
I. Calculating a 95% confidence interval
-
Critical
qt(.05, df = 134)[1] -1.656305
Interval:
Confidence interval suggests that population average BMI is well outside the range defined as normal, 18.5 - 24.99.
Finding critical
We need
-
Left or lower CI: the area to the left of
With
qt(0.05, df = 24)[1] -1.710882 -
Right or upper CI: the area to the left of
With
qt(0.95, df = 24)[1] 1.710882 -
Two-sided CI: the area to the left of
With
qt(0.975, df = 24)[1] 2.063899
Using a table
Make the
II. Formal approach to hypothesis testing
We have a mathematical model for the population.
Using this model, we calculate the probability of observing the sample statistic that was actually observed.
If this probability is extremely low, we conclude that there is something wrong with the model.
Formal approach (OI Biostat Section 4.3.1)
Steps in hypothesis testing. Details coming in subsequent slides.
Formulate null and alternative hypotheses
Specify a significance level,
Calculate a test statistic
Calculate a
State a conclusion in the context of the original problem
1. Null and alternative hypotheses
The null hypothesis (
The alternative hypothesis (
That is, the discrepancy between
1. Null and alternative…
Several possible choices for
2. Specifying a significance level
Deciding what will “extremely small” mean.
The significance level
Typically,
In the context of decision errors,
Type I error refers to incorrectly rejecting the null hypothesis.
More on this later.
Choose
3. Calculate a test statistic
The test statistic measures the discrepancy between the observed data and what would be expected if the null hypothesis were true.
- Specifically, how many standard deviations is the observed sample value from the population value under the null hypothesis?
When testing hypotheses about a mean, the test statistic is
where the test statistic
In our example
4. Calculate a
Assuming our model is correct, the
In that case, what is the probability that T = 6.3219343?
What is the probability that we would observe a result equal to or more extreme than the observed sample value, if the null hypothesis is true?
- This probability is called the
- The
- The
- A result is considered unusual under the null model if its
4. The
For a right-sided alternative,
4. The
The
The smaller the
If the
If the
What does small
The
Small
We have a really strange sample (unlikely if sample is simple random, but quite possible if it is not!)
-
There is something wrong with the model:
- Maybe we used a wrong distribution? (Assumptions not satisfied)
- Maybe the null hypothesis is false.
Typical Conclusion
If the
If the
A subtle but important point: not rejecting
What it means is that the null model is reasonable enough, and we can keep using it.
Remember: all models are wrong!
In our example
1 - pt(6.32, df = 134)[1] 1.797873e-09The
Finding the
Suppose the
-
Left-tailed test: the area to the left of
With
pt(-3.2, df = 5)[1] 0.01199759 -
Right-tailed test: the area to the right of
With
1 - pt(3.2, df = 5)[1] 0.01199759 -
Two-tailed test: twice the area to the right of
With
2*(1 - pt(3.2, df = 5))[1] 0.02399518
Using a table
With
5. Draw a conclusion
State the conclusion in the context of the original problem, using the language and units of that problem.
This is the part most often omitted, but it is the most important!
At 5% significance level, we have sufficient evidence to reject the null hypothesis that the mean BMI of the US population is 24.99.
According to our evidence, the real mean BMI of the US population is significantly higher (
Types of Errors
|
|
|
|
|---|---|---|
| reject |
type I error | desired |
| don’t reject |
desired | type II error |
Theoretical probability of type I error is the significance level
More about errors and significance levels next time.
Example
Researchers collected measurements of 64 zebra mussels (Dreissena polymorpha) from a lake in northern Michigan. The mean length of mussels in their sample was 37.5 mm, with standard deviation 7.2 mm. Use this data to find a 95% confidence interval estimating the mean length of the zebra mussels in the lake.
Example
The length of zebra mussels in certain lake in northern Michigan was previously modeled using a normal distribution with mean 39.2 mm. In an attempt to control the zebra mussel infestation, native crayfish was introduced into the lake. Two years later, researchers collected measurements of 64 zebra mussels from the lake. The mean length of their sample was 31.8 mm, with standard deviation 6.1 mm. Use this data to test the original model at 5% significance level.